Efficient Memory Management for Deep Neural Net Inference

Keywords : Deep neural networks, DNN inference, Intermediate tensors, Memory management, Tensor usage interval, Tensor usage record, Operator profile, Shared objects
Related post : https://blog.tensorflow.org/2020/10/optimizing-tensorflow-lite-runtime.html
ABSTRACT
심층 신경망 추론은 서버 전용 작업으로 간주되었지만 최신 기술 발전을 통해 추론 작업을 대기 시간에서 개인 정보 보호까지 다양한 이유로 모바일 및 임베디드 장치에 이르게 되었습니다. 이러한 장치는 컴퓨팅 성능과 배터리뿐만 아니라 열악한 physical memory 및 캐시에 의해 제한됩니다. 때문에 효율적인 메모리 관리자는 에지에서 심층 신경망 추론을 위한 중요한 요소입니다. 심층 신경망의 중간 텐서간에 메모리 버퍼를 스마트하게 공유하기위한 다양한 전략을 탐색합니다. 이를 사용하면 최신 기술보다 최대 11 % 더 작은 메모리 공간을 확보 할 수 있습니다.
1 INTRODUCTION
심층 신경망은 컴퓨터 비전, 자연어 처리, 신호 처리 등 다양한 기계 학습 문제를 해결하는 데 널리 사용됩니다. 심층 신경망을 사용하는 것은 계산 및 메모리의 리소스가 까다롭기 때문에 기술적으로 어렵지만 최근 컴퓨팅 하드웨어의 발전으로 심층 신경망을 모바일 및 임베디드 장치에서 수행 할 수 있습니다 (Lee et al., 2019; Wu et al., 2019).
심층 신경망은 CONVOLUTION 또는 SOFTMAX와 같은 계산 연산을 설명하는 노드와 연산자 간의 중간 계산 결과를 포함하는 텐서를 설명하는 간선이있는 DAG (Directed Acyclic Graph)로 나타낼 수 있습니다 (Bergstra et al., 2010). 이러한 텐서는 메모리 버퍼로 구체화됩니다. [B, H, W, C] 모양의 텐서는 B x H x W x C x sizeof(float) 크기의 메모리 버퍼로 변환됩니다. 동적 메모리 할당의 오버 헤드를 줄이기 위해 중간 텐서에 대한 메모리 버퍼는 일반적으로 모델을 실행하기 전에 할당되지만 메모리를 많이 차지할 수 있습니다. 예를 들어 Inception v3 (Szegedy et al., 2016)의 중간 텐서는 총 런타임 메모리 147MB의 37%를 차지하고 MobileNet v2 (Sandler et al., 2018)의 중간 텐서는 41MB의 63%를 차지합니다.
다행히 중간 텐서(intermediate tensors)는 메모리에 공존(co-exist) 할 필요가 없습니다. 데이터 의존성으로 인한 네트워크의 대부분의 순차 실행 덕분에 주어진 시점에서 하나의 연산자만 활성화되고 즉각적인 입력 및 출력 중간 텐서만 필요합니다. 따라서 우리는 심층 신경망 추론 엔진의 총 메모리 공간을 최적화하기 위해 메모리 버퍼를 재사용하는 아이디어를 탐구합니다. DAG가 단순한 체인의 형태인 경우 메모리 버퍼에 네트워크의 중간 텐서를 포함 할 수있는 충분한 용량이 있다고 가정하면 메모리 버퍼를 교대로 재사용 할 수 있습니다. 그러나 메모리 버퍼의 용량이 제한적이거나 네트워크에 잔여 연결이 포함된 경우 재사용 문제를 해결하기가 쉽지 않습니다 (He et al., 2016).
이 논문에서는 중간 텐서의 효율적인 메모리 공유를 위한 5가지 전략을 제시합니다. 모든 중간 텐서를 메모리에 그대로 유지하는 것에 비해 최대 10.5 배 감소하고 이전 기술에 비해 최대 11%의 메모리 소비 감소를 보여줍니다. 메모리 버퍼를 효율적으로 재사용하면 캐시 적중률이 향상되고 추론 속도가 최대 10% 향상됩니다. 이러한 전략은 신경망 추론에만 적용 할 수 있으며 중간 텐서는 살아 있어야하므로 메모리를 다시 사용할 수 없기 때문에 훈련에는 적용되지 않습니다.
2 RELATED WORK
DNN을 위한 메모리를 효율적으로 관리하는 것은 리소스가 제한된 환경뿐만 아니라 서버에도 문제가됩니다. MXNet은 병렬 연산자 실행에 안전한 메모리 할당을 위한 간단한 휴리스틱 알고리즘을 사용하여 내부 연산자 및 중간 텐서 메모리 공동 공유와 같은 메모리 소비를 줄이기 위한 여러 기술을 사용합니다 (Chen et al., 2015). 그러나 저자는 메모리 관리의 핵심 문제에 초점을 맞추지 않고 이 문제를 가장 효과적인 방법으로 해결할 수 있는 다른 알고리즘을 탐색하지 않습니다. (Chen et al., 2016)은 메모리를 위한 trading computation과 함께 유사한 기술을 사용하지만 모바일에는 적합하지 않습니다.
Caffe2의 기기 내 추론 엔진은 NNPACK 및 QNNPACK을 사용합니다 (Wu et al., 2019). 이러한 신경망 오퍼레이터 라이브러리는 최상의 데이터 레이아웃을 선택하고 오프 칩 메모리 액세스를 최적화하지만 추론 엔진의 메모리 풋 프린트를 최소화하는 데 초점을 맞추지 않습니다. (Li et al., 2016)은 유사하게 데이터 레이아웃을 활용하여 오프 칩 메모리 액세스를 최적화하고 모바일 또는 임베디드 장치만큼의 리소스 제약이 없는 서버같은 환경에 중점을 둡니다.
TensorFlow Lite (TFLite) GPU는 GPU 버퍼에 메모리 관리자를 사용합니다 (Lee et al., 2019). 이 NP-complete resource management problem(Sethi, 1975)에 대해 두 가지 근사치가 탐구되는데, 이는 레지스터 할당 문제와 유사하지만 텐서의 크기가 다르기 때문에 더 복잡합니다. (Sekiyama et al., 2018)는 2D 스트립 패킹 문제의 특별한 경우로 메모리 할당 문제를 해결합니다. 대부분의 경우를 능가하는 전략을 제시합니다.
3 DEFINITION OF TERMS
This section defines several key terms that should facilitate strategy description in the following sections.
Tensor Usage Interval of an intermediate tensor t 은 {first_op_t, last_op_t} 쌍으로 정의되며, 여기서 first_op_t 및 last opt는 각각 t를 입력 또는 출력으로 사용하는 첫 번째 및 마지막 연산자의 인덱스입니다. 인덱스는 오퍼레이터의 실행 순서이기도 한 신경망의 토폴로지 종류에서 나옵니다. 이 문서의 나머지 부분에서는 이 순서가 고정되어 있다고 가정합니다. 사용 간격이 겹치는 두 개의 텐서는 메모리를 공유 할 수 없습니다.
Tensor Usage Record of an intermediate tensor t 는 triple {first_op_t, last_op_t, size_t}로 정의됩니다. 여기서 size_t는 t의 정렬된 크기 (바이트)입니다. Figure 1은 예제 신경망과 텐서 #2의 tensor usage record을 보여줍니다. tensor usage record의 전체 세트는 Figure 2 (a)에 나와 있습니다.
Operator Profile of an operator op 은 op가 first_op_t와 last_op_t 사이에 속하도록 모든 tensor usage records t의 집합으로 정의됩니다. Figure 2 (b)는 크기별 내림차순으로 정렬된 각 연산자의 연산자 프로필을 시각화합니다.
Operator Breadth of an operator는 프로필에있는 모든 텐서 크기의 합으로 정의됩니다. 예를 들어, Figure 2 (b)의 연산자 #3은 연산자 폭이 36 + 28 + 16 = 80입니다.
The i-th Positional Maximum은 각 연산자 프로필에 대해 내림차순으로 i 번째 텐서 크기의 최대 값입니다. 예를 들어, Figure 2 (b)의 세 번째 위치 최대 값은 max (16, 16, 16, 10) = 16과 같습니다.


4 THE SHARED OBJECTS APPROACH
이 섹션과 다음 섹션에서 설명하는 메모리 공유 방법에는 크게 두 가지가 있습니다. 주어진 시간에 각 메모리 버퍼 ( "shared object")가 중간 텐서에 할당되는 first Shared Objects를 호출합니다. 사용 간격이 교차하는 두 개의 텐서가 동일한 공유 객체에 할당 될 수 없으며, 한 번에 하나 이상의 텐서에 대해 공유 객체를 사용할 수 없습니다. 공유 객체의 크기는 할당된 모든 텐서 크기 중 최대값입니다. 주요 목표는 이러한 공유 객체의 전체 크기를 최소화하는 것입니다. 이 접근 방식은 GPU 텍스처에 가장 적합합니다.
4.1 Theoretical Lower Bound
각 오퍼레이터 프로파일은 텐서 크기에 따라 비오름차순(non-increasing order)으로 정렬됩니다. 결과 할당에서 가장 큰 공유 객체는 정렬된 모든 프로필에서 가장 큰 첫 번째 요소보다 크거나 같은 크기를 가지며 두 번째로 큰 공유 객체는 정렬된 프로필에서 두 번째로 큰 요소보다 작을 수 없습니다. 이 속성은 모든 공유 객체에 적용됩니다. 공유 객체의 수는 하나의 운영자 프로필에서 가장 큰 텐서 수보다 적을 수 없습니다. 따라서 positional maximums의 합은 공유 객체 문제에 대한 이론적인 하한선입니다. 이 하한은 일부 신경망에서 수행될 수 없습니다.
4.2 Greedy by Breadth
연산자 폭(operator breadths)은 추론 중 텐서 할당 순서보다 결과 메모리 소비와 더 관련이 있습니다. 따라서 더 넓은 폭의 연산자를 실행하는 동안 메모리에 있어야하는 텐서 할당부터 시작합니다. 즉, Greedy by Breadth (Algorithm 1)입니다.
연산자는 폭 (L.4)에 따라 비오름차순으로 정렬됩니다. 이 정렬된 순서의 각 연산자에 대해, 프로필에서 텐서에 공유 객체를 할당하지만 아직 할당되지 않은 객체에 대해서만 할당합니다 (L.7). 이러한 텐서가 여러 개인 경우 크기별로 가장 큰 것부터 시작합니다. 공유 객체 s는 텐서 u가 없는 경우에만 텐서 t에 할당하기에 적합합니다. s는 u에 할당되고 사용 간격은 t와 u가 겹칩니다 (L.18-23). 공유 객체 할당 (L.12–17, 24–28)은 다음과 같이 요약 할 수 있습니다.
- size_t보다 큰(작지 않은) 적절한 공유 객체가 있는 경우 가장 작은 것을 t에 할당합니다.
- 적합한 모든 공유 객체가 size_t보다 작으면 가장 큰 크기를 size_t로 업데이트하고 t에 할당합니다.
- 적합한 공유 객체가 없는 경우 size_t 크기의 새 공유 객체를 만들고 t에 할당합니다.

알고리즘은 O (kn^2)의 런타임 복잡도를 가지며, 여기서 k와 n은 naively 구현 될 때 각각 공유 객체와 중간 텐서의 개수입니다. k는 종종 낮은 10에 있으며, n은 일반적인 신경망에서 1 또는 2 크기 정도 더 큽니다. 모든 텐서의 사용 간격을 저장하는 각 공유 객체에 대한 간격 트리(interval tree)를 사용하면 복잡성을 O (kn log (n))로 줄일 수 있습니다. Figure 3은 예제 출력입니다.

4.3 Greedy by Size
연산자 폭은 중요하지만 연산자 프로필의 텐서 크기에서 파생된 숫자입니다. 따라서 텐서 크기가 가장 중요한 기능인 Greedy by Size 전략을 탐색합니다 (Algorithm 2).
중간 텐서를 크기의 non-increasing order로 반복하고 (L.1,5), 각 텐서에 대해 Greedy by Breadth와 유사하게 할당할 적절한 공유 객체를 찾습니다 (L.8-11). 이전과 마찬가지로 처음에는 공유 객체가 없습니다 (L.2). 작은 텐서보다 더 큰 텐서를 선호하기 때문에 할당이 훨씬 쉬워집니다. 즉, 공유 객체 크기는 절대 증가하지 않고 두 단계만 남습니다.
- t에 가장 적합한 공유 객체가 있으면 할당합니다.
- 적합한 공유 객체가없는 경우 size_t 크기의 새 공유 객체를 만들고 t에 할당합니다.
Greedy by Size는 Greedy by Breadth와 복잡성이 동일합니다. 예제 출력은 Figure 4에 나와 있습니다.

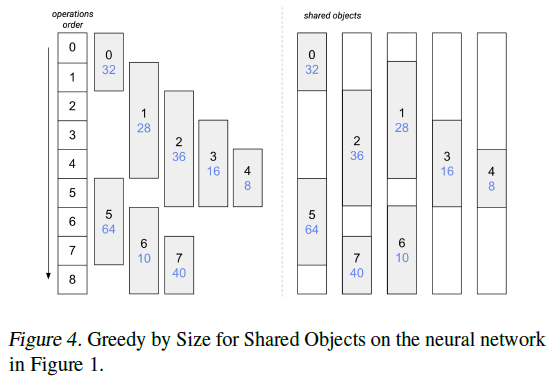
4.4 Greedy by Size Improved
Greedy by Size를 수정하는 동안, 우리는 하한에 도달하지 못하게하는 밀접한 잘못된 할당이 있음을 관찰했습니다. 비슷한 크기의 텐서에 대한 여유 공간(wiggle room)이 있다면 최적에 도달했을 수 있습니다.
공유 객체의 이론적 하한은 positional maximums에 의해 결정되므로 크기별 Greedy를 positional maximums에 따라 단계로 분할했습니다. 첫 번째 단계에서는 가장 큰 positional maximums과 같은 크기의 모든 텐서를 할당합니다. 두 번째 단계에서는 크기가 가장 큰 positional maximums보다 작지만 두 번째 최대값보다 큰 모든 텐서를 할당합니다. 세 번째 단계에서는 모든 텐서가 할당 될 때까지 두 번째 positional maximums 등과 같은 크기의 모든 텐서를 할당합니다. 우리는 한 단계의 모든 텐서가 거의 동일한 의미를 갖는 것으로 간주합니다. 이것은 다른 신경망에서 greedy algorithms을 사용한 실험의 결과를 기반으로합니다. 최종 결과는 일반적으로 이론적 하한에 매우 가깝고 대부분의 공유 객체, 특히 더 큰 객체는 종종 하한과 동일한 크기를 갖습니다.
우리가 제안하는 또 다른 개선 사항은 한 단계 내에서 텐서 할당 순서입니다. 한 단계의 텐서 크기는 거의 동일하므로 공유 객체를 사용하지 않을 때 가능한 가장 작은 시간 간격을 발생시키는 텐서 및 공유 객체 쌍을 선택합니다. 즉, 이러한 텐서 쌍이 현재 단계와 적절한 공유 객체를 형성합니다. s의 경우 t에 대한 사용 간격과 이전에 s에 할당된 텐서에서 가장 가까운 사용 간격 사이의 거리가 가능한 가장 작습니다. 즉, 텐서 t 할당에 여전히 사용할 수 있는 공유 객체를 찾았지만 텐서 t 사용 간격 직전 또는 직후에 이 공유 객체를 사용하지 않을 때의 간격이 가능한 가장 작습니다.
이러한 개선 사항은 Greedy by Size의 복잡성을 변경하지 않고 구현할 수 있습니다. 알고리즘은 2의 위치 최대 값으로 정의된 순서를 사용하여 공유 객체를 텐서에 할당합니다. Figure 5는 이 전략을 시각화합니다. 실험 결과, Greedy by Size Improved를 사용하면 개선되지 않은 원본에 비해 더 나은 결과 또는 동일한 결과를 얻을 수 있음이 확인되었습니다.

5 THE OFFSET CALCULATION APPROACH
우리는 다른 메모리 공유 방식을 Offset Calculation이라고 부르는데, 여기서 큰 메모리 청크가 미리 할당되고 중간 텐서가 메모리 블록 내의 오프셋에 의해 메모리의 일부가 제공됩니다. 주요 목표는 할당된 메모리 블록의 크기를 최소화하는 것입니다. 이 문제에 대한 솔루션은 할당된 총 메모리 측면에서 최상의 성능을 보여 주지만 CPU 메모리 또는 GPU 버퍼에만 적용 할 수 있으며 전체적으로 액세스해야하는 GPU 텍스처에는 적용 할 수 없습니다. 공유 객체 문제의 해결책은 공유 객체를 메모리에 연속적으로 배치함으로써 오프셋 계산 문제의 해결책이 될 수 있습니다. 교차하지 않는 사용 간격을 가진 텐서의 메모리 공간이 여전히 겹칠 수 있으므로 그 반대는 성립하지 않습니다.
오프셋 계산 문제는 2D 스트립 패킹 문제의 특별한 경우로 볼 수 있습니다 (Sekiyama et al., 2018). 다른 차원으로 크기를 최소화하기 위해 하나의 축으로 고정된 좌표를 가진 직사각형 항목 집합을 컨테이너에 넣습니다. 컨테이너의 높이를 할당 시간 축으로 취급한다면, 메모리 풋 프린트에 해당하는 컨테이너의 너비를 최소화해야합니다.
5.1 Theoretical Lower Bound
신경망의 연산자를 실행하는 동안 해당 프로필의 모든 텐서는 메모리에 있어야합니다. 총 크기는 연산자의 폭과 같습니다. 즉, 모든 전략은 모든 연산자 범위보다 크거나 같은 메모리 소비를 제공하고 오프셋 계산의 하한은 모든 연산자 범위 중 최대 값과 같습니다. 하한은 항상 달성 될 수는 없지만 우리의 방법은 대부분의 경우 하한을 달성합니다.
5.2 Greedy by Size for Offset Calculation
Greedy by Size는 공유 객체에서 잘 작동하므로 오프셋 계산에 유사한 방법을 사용합니다 (Algorithm 3).
먼저 텐서 사용 레코드를 크기별로 비오름차순으로 반복합니다 (L.1,6). 각 레코드에 대해 사용 간격이 현재 텐서 (L.10–13)의 사용 간격과 교차하는 이미 할당된 텐서를 확인하여 현재 텐서가 해당 간격에 맞도록 메모리에서 가장 작은 간격을 찾습니다 (L.9,14– 17). 이러한 갭이 발견되면 현재 텐서가 이 갭에 할당됩니다. 그렇지 않으면 사용 간격이 현재 텐서와 교차하는 가장 오른쪽 텐서 뒤에 할당합니다 (L.19-20). 해당 오프셋을 현재 텐서에 할당하면 Figure 6과 같이 텐서가 할당됩니다 (L.21–23).


5.3 Greedy by Breadth for Offset Calculation
Greedy by Breadth는 비슷한 방식으로 오프셋 계산을 위해 변환 할 수도 있습니다. 구체적으로:
- 모든 연산자를 폭에 따라 비오름차순으로 반복합니다.
- 이 순서의 각 연산자에 대해 아직 할당되지 않은 프로필의 모든 텐서를 크기가 비오름차순으로 반복합니다.
- 텐서의 오프셋을 계산하려면 Alg.3 에서 가장 작은 갭을 찾는 동일한 로직을 사용하십시오. (L.7–23). 이 단계가 끝나면 텐서는 할당 된 것으로 표시됩니다.
Greedy by Breadth는 크기별 Greedy에 비해 오프셋 계산에서 잘 수행되지 않지만 여전히 MobileNet v2같은 일부 네트워크에서 이전 작업을 능가합니다.
6 EVALUATION
We compare our strategies with Greedy (Lee et al., 2019), Min-cost Flow (Lee et al., 2019), and Strip Packing Bestfit (Sekiyama et al., 2018) on MobileNet v1 (Howard et al., 2017), MobileNet v2 (Sandler et al., 2018), DeepLab v3 (Chen et al., 2017), Inception v3 (Szegedy et al., 2016), PoseNet (Kendall et al., 2015), and BlazeFace (Bazarevsky et al., 2019), at 32-bit precision floating point, but the strategies can be generalized to any data type.
공유 객체에 대한 최상의 결과는 MobileNet v2를 제외한 모든 네트워크에서 Greedy by Size Improved로 나타났고 MobileNet v2는 Greedy by Breadth가 더 나았습니다(Table 1). 이전 작업과 비교할 때 우리의 전략은 최대 11% 더 나은 성과를 내고, 기존 전략에 비해 최대 7.5배 더 나은 성과를 거두었습니다. 설명된 세 가지 전략이 모두 포함된 DeepLab, Greedy by Breadth가 포함된 MobileNet v2 및 Greedy by Size Improved가 포함된 BlazeFace에서 가장 중요한 개선 사항이 확인되었습니다. 우리의 전략은 MobileNet v1, PoseNet 및 BlazeFace에 대한 이론적 하한에 도달했고 다른 네트워크는 대한 하한의 16% 이내로 도달했습니다. 공유 객체 접근 방식이 필요한 추론 엔진의 경우 기본적으로 Greedy by Size Improved를 사용하는 것이 좋습니다.
Offset Calculation의 경우 Greedy by Size는 Table 2에 표시된대로 가장 잘 수행됩니다. 여전히 하한의 8 % 내에있는 DeepLab을 제외하고 모든 신경망에서 이론적 하한을 달성합니다. 또한 Greedy보다 중간 텐서에 대해 최대 25 % 적은 메모리를 사용하고 Strip Packing Bestfit보다 최대 7.7%, 기본(naive) 전략보다 최대 10.5배 적은 메모리 할당을 제공합니다. DeepLab의 경우에만 Strip Packing Bestfit은 이론적 하한에 매우 가까운 7.2% 더 나은 할당을 보여줍니다. 오프셋 계산 방식이 필요한 추론 엔진의 경우 첫 번째 추론 전에 크기별 Greedy와 Strip Packing Bestfit을 모두 평가하고 우수한 성능 전략을 선택하는 것이 좋습니다.

7 CONCLUSION
에지에서 추론 엔진의 메모리 공간을 최소화하기 위해 DNN의 중간 텐서간 메모리 버퍼를 효율적으로 공유하기위한 5 가지 새로운 전략을 제시했습니다. 실험에서 우리의 전략은 추론 런타임의 메모리 공간이 이론적 하한과 같거나 그에 가깝다는 것을 보여주었습니다.
두 가지 접근 방식에 대해 제시된 전략은 충분히 빠르므로 (대부분의 네트워크에서 몇 밀리 초) 가장 작은 메모리 풋프린트를 위해 런타임에 탐색 할 수 있습니다. 일반적으로 CPU 추론 또는 버퍼를 사용한 GPU 추론에서, Offset Calculation problem에 대한 두 가지 최상의 전략인 Greedy by Size와 Strip Packing Bestfit을 탐색하는 것이 좋습니다. 텍스처를 사용한 GPU 추론같은 공유 객체 문제의 경우, Greedy by Size Improved 및 Greedy by Breadth는 사전 추론 탐색에 권장됩니다.
제시된 전략은 중간 텐서의 크기를 미리 알고 있다고 가정합니다. 이 가정은 동적으로 크기가 변경되는 중간 텐서를 포함하는 단기 기억 단위가 긴 반복 신경망 (Hochreiter & Schmidhuber, 1997)에서는 다를 수 있습니다. 이러한 경우 알고리즘을 여러 번 실행하여 모든 실행의 할당에 대한 정보를 한 곳에서 저장해야합니다. 첫 번째 실행은 처음에 크기가 알려진 텐서만 할당하고 두 번째 실행은 첫 번째 동적 텐서를 계산 한 후 크기가 알려지는 텐서를 할당합니다.



